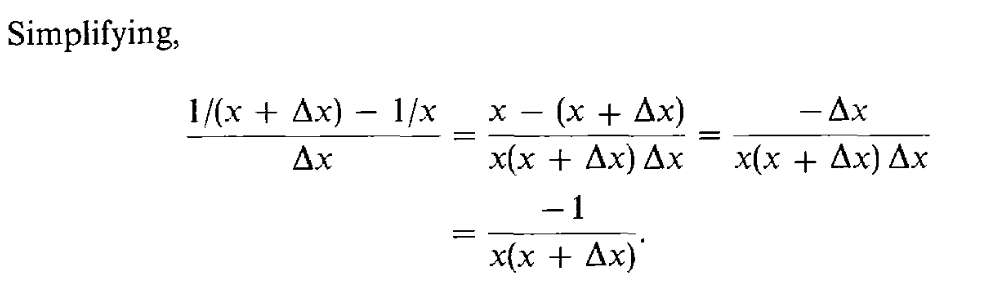notes

In here are the list of things I did for a particular hour or day. Also included here are the screenshots of games I played, or videos I watched or listened to, or just random things I stumbled upon. I'll occasionally write down what I'm thinking, or things I'm planning to do.

[ 2024-02-16 ]

14:20 [link] [context] #math

I'm wondering now, why do I need to add the two fractions together before I could simplify it. Isn't there another way? That does sounds like a math trick that I must do without knowing why. That's what I tried before, but I couldn't get any further:

   [1/(x+y) - 1/x]/y               
 = [(x+y)~ - x~]y~
 = (x+y)~y~ - x~y~
 = [(x+y)y]~ - x~y~
 = [xy+yy]~ - x~y~     // how do I go from this...
 ...
 = -(x+y)~x~           // to this

Maybe, there's a theorem that I could use for this?

   x~ + y~ = (x+y)x~y~
   x~ + y~ = [(x+y)~x]~y~
   x~ + y~ = [(x+y)~x]~y~      // TODO:

 xy~ = (x~y)~          // ooh, this is actually true
 x~y = (xy~)~          // woah, this  holds as well
 xy = (x~y~)~          // this too!?!? 
 xyz = (x~y~z~)~       // cool, it generalizes to arbitrary number of terms
                       // actually ~ behaves a like  de morgan's law

Ahaaha, did I just discover/invent new theorems for my own operator? This is actually pretty neat stuffs. My mind feels a bit blown. I didn't think math would be this fun. Yeah, with this new theorem, I think I could actually do solve the equation without relying on the math trick.

🕛 12:35

🕛 12:34

🕛 12:33

🕚 11:21

11:04 [link] [context] #math

   x~ + y~
 = (x + y)/(x*y)

Okay, I understand now, it really is just a simple fraction rule. Three things of note:

   x   numerator
 -----
   y   denominator

- two fractions can be added together if they have the same denominator - for any a, a/a = 1 - for any a, a*1 = a

To solve `1/x + 1/y`, I just need to make them have the same denominator:

   1/x + 1/y
 = (1/x)(y/y) + (1/y)(x/x)
 = y/xy + x/xy
 = (x+y)/xy

-----

Now I just need to translate this to exponential notation:

   x~ + y~
 = x~yy~ + y~xx~
 = (yy~ + y~x)x~
 = (x+y)x~y~

There, I solved it without needing special rules like "same-denominator fractions can be added" or "dividing x/y by z is the same as x/yz".

----

Back to the previous problem, I need to simplify `(1/(x+y) - 1/x)/y`:

Simplify the numerator first

   1/(x+y) - 1/x               
 = (x+y)~ + -x~                // (A)
 = (x+y)~xx~ + -x~(x+y)(x+y)~
 = (x+y)~xx~ + -x~(x+y)(x+y)~  // common: x~,(x+y)~
 = [ xx~ + -x~(x+y) ](x+y)~
 = [ x + -(x+y) ](x+y)~x~
 = [ x + -x -y) ](x+y)~x~
 = -y(x+y)~x~                 //  (B)

   (1/(x+y) - 1/x)/y
 = [ (x+y)~ + -x~ ]y~       // (A) times y~
 = [ -y(x+y)~x~   ]y~       // replaced (A) with (B)
 = -(x+y)~x~                // yy~ are inverses, so yy~ = 1
 = -1/(x+y)*x

Aha, now I got the same equation as shown in the book.

----

I'm still not sure if avoiding fractional notation is better, but at least so far I've managed to avoid relying on special rules to do algebraic simplifications. I still don't know how the book was able to get `-1/(x+y)*x`, it just seems "magic" for me. Well actually, looking closer, the book did use the same trick by making both terms use the same denominator. It only just skipped lots of steps in between.

🕚 11:03

🕙 10:29

🕙 10:28

🕖 07:21

🕒 03:58